imaging::SimpleEquationAdaptor< equation_t > Class Template Reference
[Equations]

Converts a SimpleEquationInterface object into an EquationInterface object. More...

#include <SimpleEquationAdaptor.hpp>

Inheritance diagram for imaging::SimpleEquationAdaptor< equation_t >:

imaging::EquationInterface< equation_t::fem_types >

List of all members.

Public Member Functions

const std::size_t system_size () const
 SimpleEquationAdaptor (const equation_t &equation)
float_t stiffness_matrix (std::size_t equation, std::size_t component, std::size_t i, std::size_t j, std::size_t integrator_node, const FemKernel< fem_types > &kernel) const
float_t force_vector (std::size_t equation, std::size_t i, std::size_t integrator_node, const FemKernel< fem_types > &kernel) const
float_t stiffness_matrix_at_boundary (std::size_t equation, std::size_t component, std::size_t i, std::size_t j, std::size_t integrator_node, const FemKernel< fem_types > &kernel) const
float_t force_vector_at_boundary (std::size_t equation, std::size_t i, std::size_t integrator_node, const FemKernel< fem_types > &kernel) const
bool sanity_check_stiffness_matrix (const FemKernel< fem_types > &kernel, std::string &error_message) const
bool sanity_check_force_vector (const FemKernel< fem_types > &kernel, std::string &error_message) const

Detailed Description

template<class equation_t>
class imaging::SimpleEquationAdaptor< equation_t >

Converts a SimpleEquationInterface object into an EquationInterface object.

This class implements EquationInterface and but can be instantiated for a class implementing SimpleEquationInterface. I.e. it enables SimpleEquationInterface objects to be used in functions requiring EquationInterface objects. In the following example this is illustrated for Assembler::assembly(): 

  img::Grid<img::fem_2d_square_types> grid;
  // construct grid...
  
  SomeSimpleEquation<img::fem_2d_square_types> simple_equation;
  // provide data (i.e. boundary data, right hand side) to the equation...
  
  img::Assembler<img::fem_2d_square_types>
  img::ublas::compressed_matrix<img::float_t> stiffness_matrix;
  img::ublas::vector<img::float_t> force_vector;
  
  img::SimpleEquationAdaptor< SomeSimpleEquation<img::fem_2d_square_types> >
    equation(simple_equation);
    
  assembler.assemble(equation, grid, stiffness_matrix, force_vector);

Constructor & Destructor Documentation

template<class equation_t>
imaging::SimpleEquationAdaptor< equation_t >::SimpleEquationAdaptor ( const equation_t &  equation  )  [inline]

Constructs a SimpleEquationAdaptor from equation. The class equation_t must implement (and should be derived from) SimpleEquationInterface.

Member Function Documentation

template<class equation_t>
const std::size_t imaging::SimpleEquationAdaptor< equation_t >::system_size (  )  const [inline]

Returns the number of equations in this system of PDEs. For scalar PDEs this is 1.

Reimplemented from imaging::EquationInterface< equation_t::fem_types >.

template<class equation_t>
float_t imaging::SimpleEquationAdaptor< equation_t >::stiffness_matrix ( std::size_t  k,
std::size_t  l,
std::size_t  i,
std::size_t  j,
std::size_t  integrator_node,
const FemKernel< fem_types > &  kernel 
) const [inline]

Computes the contribution of the integral 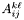$A^{k\ell}_{ij}$ in integrator_node on the current element of kernel. The node indices i and j are node indices on the element, not global indices.

As kernel is set to the current element, in the implementation of this function all relevant values of the shape functions and the element transform can be retrieved from kernel via the indices i, j and integrator_node. One can also obtain the FE grid from the kernel (FemKernel::grid()) and use its interpolation methods (passing the already correctly initialized kernel to them).

Reimplemented from imaging::EquationInterface< equation_t::fem_types >.

References imaging::FemKernel< fem_types >::is_boundary_node(), imaging::FemKernel< fem_types >::shape_gradient(), and imaging::FemKernel< fem_types >::shape_value().

template<class equation_t>
float_t imaging::SimpleEquationAdaptor< equation_t >::force_vector ( std::size_t  k,
std::size_t  i,
std::size_t  integrator_node,
const FemKernel< fem_types > &  kernel 
) const [inline]

Computes the contribution of the integral 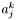$a^k_j$ in integrator_node on the current element of kernel. The node index i is the node index on the element, not a global index.

As kernel is set to the current element, in the implementation of this function all relevant values of the shape functions and the element transform can be retrieved from kernel via the indices i and integrator_node. One can also obtain the FE grid from the kernel (FemKernel::grid()) and use its interpolation methods (passing the already correctly initialized kernel to them).

Reimplemented from imaging::EquationInterface< equation_t::fem_types >.

References imaging::FemKernel< fem_types >::is_boundary_node(), imaging::FemKernel< fem_types >::shape_gradient(), and imaging::FemKernel< fem_types >::shape_value().

template<class equation_t>
float_t imaging::SimpleEquationAdaptor< equation_t >::stiffness_matrix_at_boundary ( std::size_t  k,
std::size_t  l,
std::size_t  i,
std::size_t  j,
std::size_t  integrator_node,
const FemKernel< fem_types > &  kernel 
) const [inline]

Computes the contribution of the integral 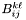$B^{k\ell}_{ij}$ in integrator_node on the current boundary element of kernel. The node indices i and j are node indices on the element, not global indices.

As kernel is set to the current boundary element, in the implementation of this function all relevant values of the shape functions and the element transform can be retrieved from kernel via the indices i, j and integrator_node. One can also obtain the FE grid from the kernel (FemKernel::grid()) and use its interpolation methods (passing the already correctly initialized kernel to them).

Reimplemented from imaging::EquationInterface< equation_t::fem_types >.

References imaging::FemKernel< fem_types >::boundary_transform_determinant(), imaging::FemKernel< fem_types >::shape_boundary_derivative(), and imaging::FemKernel< fem_types >::shape_boundary_value().

template<class equation_t>
float_t imaging::SimpleEquationAdaptor< equation_t >::force_vector_at_boundary ( std::size_t  k,
std::size_t  i,
std::size_t  integrator_node,
const FemKernel< fem_types > &  kernel 
) const [inline]

Computes the contribution of the integral 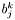$b^k_j$ in integrator_node on the current element of kernel. The node index i is the node index on the element, not a global index.

As kernel is set to the current boundary element, in the implementation of this function all relevant values of the shape functions and the element transform can be retrieved from kernel via the indices i and integrator_node. One can also obtain the FE grid from the kernel (FemKernel::grid()) and use its interpolation methods (passing the already correctly initialized kernel to them).

Reimplemented from imaging::EquationInterface< equation_t::fem_types >.

References imaging::FemKernel< fem_types >::shape_boundary_value().

template<class equation_t>
bool imaging::SimpleEquationAdaptor< equation_t >::sanity_check_force_vector ( const FemKernel< fem_types > &  kernel,
std::string &  error_message 
) const [inline]

Checks if the dimension of the data corresponds to the dimension of the grid stored in kernel for the assembly of the force vector.

This function is called by the assemble routine right before the assembly of the force vector. It should return false if data which is necessary for the assembly of the force vector is still missing. Otherwise, return true;

Reimplemented from imaging::EquationInterface< equation_t::fem_types >.

The documentation for this class was generated from the following file:
Generated on Tue Feb 10 10:01:31 2009 for imaging2 by  doxygen 1.5.5