imaging::SimpleEquationInterface< fem_types_t > Class Template Reference
[Equations]

Abstract base class of scalar, elliptic PDEs in divergence form. More...

#include <SimpleEquationInterface.hpp>

List of all members.

Public Types

enum boundary_data_types {
NO_BOUNDARY_DATA, IMPLICIT_NEUMANN_DATA, NEUMANN_DATA, DIRICHLET_DATA,
MIXED_DATA
}

typedef fem_types_t fem_types

typedef ublas::fixed_matrix
< float_t,
fem_types::data_dimension,
fem_types::data_dimension > matrix_coefficient_t

Public Member Functions

void stiffness_matrix (std::size_t integrator_node, const FemKernel< fem_types > &kernel, matrix_coefficient_t &A, ublas::fixed_vector< float_t, fem_types::data_dimension > &a, ublas::fixed_vector< float_t, fem_types::data_dimension > &b, float_t &c) const

void force_vector (std::size_t integrator_node, const FemKernel< fem_types > &kernel, float_t &f, ublas::fixed_vector< float_t, fem_types::data_dimension > &g) const

void stiffness_matrix_at_boundary (std::size_t integrator_node, const FemKernel< fem_types > &kernel, float_t &h) const

void force_vector_at_boundary (std::size_t integrator_node, const FemKernel< fem_types > &kernel, float_t &v) const

bool sanity_check_stiffness_matrix (const FemKernel< fem_types > &kernel, std::string &error_message) const

bool sanity_check_force_vector (const FemKernel< fem_types > &kernel, std::string &error_message) const

Static Public Attributes

static const bool a_active = true

static const bool b_active = true

static const bool c_active = true

static const bool f_active = true

static const bool g_active = true

static const size_t boundary_data_type

Detailed Description

template<class fem_types_t>
class imaging::SimpleEquationInterface< fem_types_t >

Abstract base class of scalar, elliptic PDEs in divergence form.

Derive this interface to solve a scalar, elliptic PDE in divergence form, i.e.

$- \nabla \cdot (A \nabla u + \vec a u ) + \vec b \cdot \nabla u + c u = f - \nabla \cdot \vec g \quad \textrm{on} \quad \Omega\,.$

The weak formulation of the above problem reads as

$\int_\Omega (A \nabla u + \vec a u ) \nabla \phi + \int_\Omega \vec b \cdot \nabla u \phi + \int_\Omega c u \phi = \int_\Omega f \phi + \int_\Omega \vec g \nabla \phi \,,$

for a test function 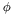$\phi$ with compact support.

Depending on the boundary conditions (i.e. on the value of the constant boundary_data_type ), this class implements five different weak formulations of boundary value problems.

boundary_data_type == NO_BOUNDARY_DATA
$\int_\Omega (A \nabla u + \vec a u ) \nabla \psi + \int_\Omega \vec b \cdot \nabla u \psi + \int_\Omega c u \psi = \int_\Omega f \psi + \int_\Omega \vec g \nabla \psi \,,$
for a test function 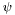$\psi$ (without compact support). This implies the boundary conditions
$\frac{\partial}{\partial \vec n}(A \nabla u + \vec a u) = 0 \quad \textrm{on} \quad \partial \Omega\,.$

boundary_data_type == IMPLICIT_NEUMANN_DATA
$\int_\Omega (A \nabla u + \vec a u ) \nabla \psi + \int_\Omega \vec b \cdot \nabla u \psi + \int_\Omega c u \psi = \int_\Omega f \psi + \int_\Omega \vec g \nabla \psi - \int_{\partial \Omega} v \psi \,,$
for a test function 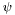$\psi$ (without compact support). This implies the boundary conditions
$\frac{\partial}{\partial \vec n}(A \nabla u + \vec a u) = v \quad \textrm{on} \quad \partial \Omega\,.$

boundary_data_type == NEUMANN_DATA
$\int_\Omega (A \nabla u + \vec a u ) \nabla \phi + \int_\Omega \vec b \cdot \nabla u \phi + \int_\Omega c u \phi = \int_\Omega f \phi + \int_\Omega \vec g \nabla \phi \,,$
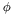for a test function $\phi$ (with compact support) and
$\int_{\partial \Omega} \frac{\partial u}{\partial \vec n} \psi = \int_{\partial \Omega} v \psi\,,$
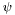for a test function $\psi$ (without compact support). This implies the boundary conditions
$\frac{\partial u}{\partial \vec n} = v \quad \textrm{on} \quad \partial \Omega\,.$

boundary_data_type == DIRICHLET_DATA
$\int_\Omega (A \nabla u + \vec a u ) \nabla \phi + \int_\Omega \vec b \cdot \nabla u \phi + \int_\Omega c u \phi = \int_\Omega f \phi + \int_\Omega \vec g \nabla \phi \,,$
for a test function 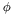$\phi$ (with compact support) and
$\int_{\partial \Omega} u \psi = \int_{\partial \Omega} v \psi\,,$
for a test function 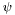$\psi$ (without compact support). This implies the boundary conditions
$u = v \quad \textrm{on} \quad \partial \Omega\,.$

boundary_data_type == MIXED_DATA
$\int_\Omega (A \nabla u + \vec a u ) \nabla \phi + \int_\Omega \vec b \cdot \nabla u \phi + \int_\Omega c u \phi = \int_\Omega f \phi + \int_\Omega \vec g \nabla \phi \,,$
for a test function 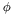$\phi$ (with compact support) and
$\int_{\partial \Omega} \frac{\partial u}{\partial \vec n} \psi + \int_{\partial \Omega} h u \psi = \int_{\partial \Omega} v \psi\,,$
for a test function 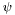$\psi$ (without compact support). This implies the boundary conditions
$\frac{\partial u}{\partial \vec n} + h u = v \quad \textrm{on} \quad \partial \Omega\,.$

Member Typedef Documentation

template<class fem_types_t>

typedef fem_types_t imaging::SimpleEquationInterface< fem_types_t >::fem_types

The fem_types for which this class template was instantiated.

template<class fem_types_t>

typedef ublas::fixed_matrix<float_t, fem_types::data_dimension, fem_types::data_dimension> imaging::SimpleEquationInterface< fem_types_t >::matrix_coefficient_t

Defines the type of matrix as passed to A(). If A() returns a diagonal matrix choosing an appropriate type to store this matrix might yield a speed-up (in particular in higher dimensions; in the plane the difference will most probably neglible).

Reimplemented in imaging::DiffusionStep< fem_types >, imaging::GeodesicActiveContourStep< fem_types >, imaging::McmStep< fem_types >, imaging::PoissonEquation< fem_types >, and imaging::TvFlowStep< fem_types >.

Member Enumeration Documentation

template<class fem_types_t>

enum imaging::SimpleEquationInterface::boundary_data_types

Different kinds of boundary data. A detailed description is given in the general part of the class documentation.

Enumerator:

NO_BOUNDARY_DATA	No boundary data. This implies a homogenous condition depending on the equation.
IMPLICIT_NEUMANN_DATA	The same as NO_BOUNDARY_DATA, but with a possible non-homogenous condition.
NEUMANN_DATA	Neumann conditions.
DIRICHLET_DATA	Dirichlet conditions.
MIXED_DATA	Robin conditions.

Member Function Documentation

template<class fem_types_t>

void imaging::SimpleEquationInterface< fem_types_t >::stiffness_matrix	(	std::size_t	integrator_node,
		const FemKernel< fem_types > &	kernel,
		matrix_coefficient_t &	A,
		ublas::fixed_vector< float_t, fem_types::data_dimension > &	a,
		ublas::fixed_vector< float_t, fem_types::data_dimension > &	b,
		float_t &	c
	)			const

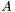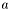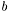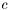Evaluates $A$ , $a$ , $b$ and $c$ in integrator_node on the current element of kernel.

As kernel is set to the current element, in the implementation of this function all relevant values of the shape functions and the element transform can be retrieved from kernel via integrator_node. One can also obtain the FE grid from the kernel (FemKernel::grid()) and use its interpolation methods (passing the already correctly initialized kernel to them).

Reimplemented in imaging::DiffusionStep< fem_types >, imaging::GeodesicActiveContourStep< fem_types >, imaging::McmStep< fem_types >, imaging::PoissonEquation< fem_types >, and imaging::TvFlowStep< fem_types >.

template<class fem_types_t>

void imaging::SimpleEquationInterface< fem_types_t >::force_vector	(	std::size_t	integrator_node,
		const FemKernel< fem_types > &	kernel,
		float_t &	f,
		ublas::fixed_vector< float_t, fem_types::data_dimension > &	g
	)			const

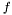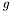Evaluates $f$ and $g$ in integrator_node on the current element of kernel.

As kernel is set to the current element, in the implementation of this function all relevant values of the shape functions and the element transform can be retrieved from kernel via integrator_node. One can also obtain the FE grid from the kernel (FemKernel::grid()) and use its interpolation methods (passing the already correctly initialized kernel to them).

Reimplemented in imaging::DiffusionStep< fem_types >, imaging::GeodesicActiveContourStep< fem_types >, imaging::McmStep< fem_types >, imaging::PoissonEquation< fem_types >, and imaging::TvFlowStep< fem_types >.

template<class fem_types_t>

void imaging::SimpleEquationInterface< fem_types_t >::stiffness_matrix_at_boundary	(	std::size_t	integrator_node,
		const FemKernel< fem_types > &	kernel,
		float_t &	h
	)			const `[inline]`

Evaluates 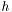$h$ in integrator_node on the current element of kernel.

As kernel is set to the current element, in the implementation of this function all relevant values of the shape functions and the element transform can be retrieved from kernel via integrator_node. One can also obtain the FE grid from the kernel (FemKernel::grid()) and use its interpolation methods (passing the already correctly initialized kernel to them).

template<class fem_types_t>

void imaging::SimpleEquationInterface< fem_types_t >::force_vector_at_boundary	(	std::size_t	integrator_node,
		const FemKernel< fem_types > &	kernel,
		float_t &	v
	)			const `[inline]`

Evaluates 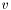$v$ in integrator_node on the current element of kernel.

As kernel is set to the current element, in the implementation of this function all relevant values of the shape functions and the element transform can be retrieved from kernel via integrator_node. One can also obtain the FE grid from the kernel (FemKernel::grid()) and use its interpolation methods (passing the already correctly initialized kernel to them).

Reimplemented in imaging::PoissonEquation< fem_types >.

template<class fem_types_t>

bool imaging::SimpleEquationInterface< fem_types_t >::sanity_check_stiffness_matrix	(	const FemKernel< fem_types > &	kernel,
		std::string &	error_message
	)			const `[inline]`

Checks if the dimension of the data corresponds to the dimension of the grid stored in kernel for the assembly of the stiffness matrix.

This function is called by the assemble routine right before the assembly of the stiffness matrix. It should return false if data which is necessary for the assembly of the stiffness matrix is still missing. Otherwise, return true;

Reimplemented in imaging::DiffusionStep< fem_types >, imaging::GeodesicActiveContourStep< fem_types >, imaging::McmStep< fem_types >, imaging::PoissonEquation< fem_types >, and imaging::TvFlowStep< fem_types >.

template<class fem_types_t>

bool imaging::SimpleEquationInterface< fem_types_t >::sanity_check_force_vector	(	const FemKernel< fem_types > &	kernel,
		std::string &	error_message
	)			const `[inline]`

Checks if the dimension of the data corresponds to the dimension of the grid stored in kernel for the assembly of the force vector.

This function is called by the assemble routine right before the assembly of the force vector. It should return false if data which is necessary for the assembly of the force vector is still missing. Otherwise, return true;

Reimplemented in imaging::DiffusionStep< fem_types >, imaging::GeodesicActiveContourStep< fem_types >, imaging::McmStep< fem_types >, imaging::PoissonEquation< fem_types >, and imaging::TvFlowStep< fem_types >.

Member Data Documentation

template<class fem_types_t>

const bool imaging::SimpleEquationInterface< fem_types_t >::a_active = true [static]

Must be set to true if 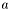$a$ can be non-zero. If it is false, 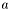$a$ will not be evaluated in the assembly functions to save computation time.

Reimplemented in imaging::DiffusionStep< fem_types >, imaging::GeodesicActiveContourStep< fem_types >, imaging::McmStep< fem_types >, imaging::PoissonEquation< fem_types >, and imaging::TvFlowStep< fem_types >.

template<class fem_types_t>

const bool imaging::SimpleEquationInterface< fem_types_t >::b_active = true [static]

Must be set to true if 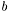$b$ can be non-zero. If it is false, 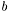$b$ will not be evaluated in the assembly functions to save computation time.

Reimplemented in imaging::DiffusionStep< fem_types >, imaging::GeodesicActiveContourStep< fem_types >, imaging::McmStep< fem_types >, imaging::PoissonEquation< fem_types >, and imaging::TvFlowStep< fem_types >.

template<class fem_types_t>

const bool imaging::SimpleEquationInterface< fem_types_t >::c_active = true [static]

Must be set to true if 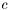$c$ can be non-zero. If it is false, 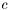$c$ will not be evaluated in the assembly functions to save computation time.

Reimplemented in imaging::DiffusionStep< fem_types >, imaging::GeodesicActiveContourStep< fem_types >, imaging::McmStep< fem_types >, imaging::PoissonEquation< fem_types >, and imaging::TvFlowStep< fem_types >.

template<class fem_types_t>

const bool imaging::SimpleEquationInterface< fem_types_t >::f_active = true [static]

Must be set to true if 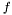$f$ can be non-zero. If it is false, 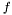$f$ will not be evaluated in the assembly functions to save computation time.

Reimplemented in imaging::DiffusionStep< fem_types >, imaging::GeodesicActiveContourStep< fem_types >, imaging::McmStep< fem_types >, imaging::PoissonEquation< fem_types >, and imaging::TvFlowStep< fem_types >.

template<class fem_types_t>

const bool imaging::SimpleEquationInterface< fem_types_t >::g_active = true [static]

Must be set to true if 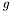$g$ can be non-zero. If it is false, 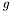$g$ will not be evaluated in the assembly functions to save computation time.

Reimplemented in imaging::DiffusionStep< fem_types >, imaging::GeodesicActiveContourStep< fem_types >, imaging::McmStep< fem_types >, imaging::PoissonEquation< fem_types >, and imaging::TvFlowStep< fem_types >.

template<class fem_types_t>

const size_t imaging::SimpleEquationInterface< fem_types_t >::boundary_data_type [static]

The type of boundary conditions for this equation as defined in SimpleEquationInterface::boundary_data_types.

Reimplemented in imaging::DiffusionStep< fem_types >, imaging::GeodesicActiveContourStep< fem_types >, imaging::McmStep< fem_types >, imaging::PoissonEquation< fem_types >, and imaging::TvFlowStep< fem_types >.

The documentation for this class was generated from the following file:

imaging2/fem/equation/SimpleEquationInterface.hpp


Public Types
enum	boundary_data_types { NO_BOUNDARY_DATA, IMPLICIT_NEUMANN_DATA, NEUMANN_DATA, DIRICHLET_DATA, MIXED_DATA }
typedef fem_types_t	fem_types
typedef ublas::fixed_matrix < float_t, fem_types::data_dimension, fem_types::data_dimension >	matrix_coefficient_t
Public Member Functions
void	stiffness_matrix (std::size_t integrator_node, const FemKernel< fem_types > &kernel, matrix_coefficient_t &A, ublas::fixed_vector< float_t, fem_types::data_dimension > &a, ublas::fixed_vector< float_t, fem_types::data_dimension > &b, float_t &c) const
void	force_vector (std::size_t integrator_node, const FemKernel< fem_types > &kernel, float_t &f, ublas::fixed_vector< float_t, fem_types::data_dimension > &g) const
void	stiffness_matrix_at_boundary (std::size_t integrator_node, const FemKernel< fem_types > &kernel, float_t &h) const
void	force_vector_at_boundary (std::size_t integrator_node, const FemKernel< fem_types > &kernel, float_t &v) const
bool	sanity_check_stiffness_matrix (const FemKernel< fem_types > &kernel, std::string &error_message) const
bool	sanity_check_force_vector (const FemKernel< fem_types > &kernel, std::string &error_message) const
Static Public Attributes
static const bool	a_active = true
static const bool	b_active = true
static const bool	c_active = true
static const bool	f_active = true
static const bool	g_active = true
static const size_t	boundary_data_type

imaging::SimpleEquationInterface< fem_types_t > Class Template Reference [Equations]

Public Types

Public Member Functions

Static Public Attributes

Detailed Description

template<class fem_types_t> class imaging::SimpleEquationInterface< fem_types_t >

Member Typedef Documentation

Member Enumeration Documentation

Member Function Documentation

Member Data Documentation

imaging::SimpleEquationInterface< fem_types_t > Class Template Reference
[Equations]

template<class fem_types_t>
class imaging::SimpleEquationInterface< fem_types_t >