B-Spline Module
Classes | |
| class | imaging::Bspline< DATA_t > |
| Class template for B-Splines of arbitrary data type. More... | |
| class | imaging::PeriodicBspline< DATA_t > |
| Class template for periodic B-Splines of arbitrary data type. More... | |
| class | imaging::imaging::xml_handler< PeriodicBspline< DATA_t > > |
| class | imaging::imaging::xml_handler< Bspline< DATA_t > > |
Functions | |
| GraphicsInterface & | imaging::operator<< (GraphicsInterface &out, const Bspline< ublas::fixed_vector< float_t, 2 > > &curve) |
| GraphicsInterface & | imaging::operator<< (GraphicsInterface &out, const PeriodicBspline< ublas::fixed_vector< float_t, 2 > > &curve) |
| void | imaging::basis_spline (size_t i, Bspline< float_t > &spline) |
| void | imaging::basis_spline (size_t i, PeriodicBspline< float_t > &spline) |
| void | imaging::interpolation_matrix (const Bspline< float_t > &spline, const ublas::vector< float_t > &values, ublas::compressed_matrix< float_t > &matrix) |
| void | imaging::interpolation_matrix (const PeriodicBspline< float_t > &spline, const ublas::vector< float_t > &values, ublas::compressed_matrix< float_t > &matrix) |
| void | imaging::basis_spline_matrix (const PeriodicBspline< float_t > &spline, const ublas::vector< float_t > &values, ublas::compressed_matrix< float_t > &matrix) |
| void | imaging::basis_spline_matrix (const Bspline< float_t > &spline, const ublas::vector< float_t > &values, ublas::compressed_matrix< float_t > &matrix) |
Detailed Description
The B-spline module includes classes for B-spline and periodic B-spline functions. This includes spline functions and curves of arbitrary dimension. The module provides functions to read/write B-splines from/to XML files and to display planar spline curves. It contains utility functions to solve the spline interpolation problem.Function Documentation
| void imaging::basis_spline | ( | size_t | i, | |
| PeriodicBspline< float_t > & | spline | |||
| ) |
#include <spline/utilities.hpp>
Sets the i-th spline coefficient of spline to 1 and all the others to 0.
Referenced by imaging::basis_spline().
| void imaging::basis_spline | ( | size_t | i, | |
| Bspline< float_t > & | spline | |||
| ) |
#include <spline/utilities.hpp>
Sets the i-th spline coefficient of spline to 1 and all the others to 0.
References imaging::basis_spline().
| void imaging::basis_spline_matrix | ( | const Bspline< float_t > & | spline, | |
| const ublas::vector< float_t > & | values, | |||
| ublas::compressed_matrix< float_t > & | matrix | |||
| ) |
#include <spline/utilities.hpp>
Computes the matrix which is the result of the spline interpolation problem. Assume a B-spline function
![\[ s(\tau) = \sum_{i = 0}^n a_i b_i(\tau) \]](form_94.png)
and consider the interpolation problem
![\[ s(\tau_k) = y_k\,,\quad 0 \leq k \leq N\,. \]](form_95.png)
Then the least squares solution of this problem is defined by the system of linear equations
![\[ \sum_{i=0}^n a_i \underbrace{\sum_{k=0}^N b_i(\tau_k)b_j(\tau_k)}_{A_{ij}} = \sum_{j=0}^N \underbrace{b_j(\tau_k)}_{B_{jk}} y_k\,,\quad 0 \leq j \leq n\,. \]](form_96.png)
If 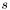 is given by spline and
is given by spline and 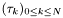 by values, then this function writes
by values, then this function writes 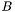 to matrix.
to matrix.
| void imaging::basis_spline_matrix | ( | const PeriodicBspline< float_t > & | spline, | |
| const ublas::vector< float_t > & | values, | |||
| ublas::compressed_matrix< float_t > & | matrix | |||
| ) |
#include <spline/utilities.hpp>
Computes the matrix which is the result of the spline interpolation problem. Assume a B-spline function
![\[ s(\tau) = \sum_{i = 0}^n a_i b_i(\tau) \]](form_94.png)
and consider the interpolation problem
![\[ s(\tau_k) = y_k\,,\quad 0 \leq k \leq N\,. \]](form_95.png)
Then the least squares solution of this problem is defined by the system of linear equations
![\[ \sum_{i=0}^n a_i \underbrace{\sum_{k=0}^N b_i(\tau_k)b_j(\tau_k)}_{A_{ij}} = \sum_{j=0}^N \underbrace{b_j(\tau_k)}_{B_{jk}} y_k\,,\quad 0 \leq j \leq n\,. \]](form_96.png)
If 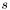 is given by spline and
is given by spline and 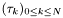 by values, then this function writes
by values, then this function writes 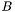 to matrix.
to matrix.
| void imaging::interpolation_matrix | ( | const PeriodicBspline< float_t > & | spline, | |
| const ublas::vector< float_t > & | values, | |||
| ublas::compressed_matrix< float_t > & | matrix | |||
| ) |
#include <spline/utilities.hpp>
Computes the matrix which is the result of the spline interpolation problem. Assume a B-spline function
![\[ s(\tau) = \sum_{i = 0}^n a_i b_i(\tau) \]](form_94.png)
and consider the interpolation problem
![\[ s(\tau_k) = y_k\,,\quad 0 \leq k \leq N\,. \]](form_95.png)
Then the least squares solution of this problem is defined by the system of linear equations
![\[ \sum_{i=0}^n a_i \underbrace{\sum_{k=0}^N b_i(\tau_k)b_j(\tau_k)}_{A_{ij}} = \sum_{j=0}^N \underbrace{b_j(\tau_k)}_{B_{jk}} y_k\,,\quad 0 \leq j \leq n\,. \]](form_96.png)
If 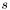 is given by spline and
is given by spline and 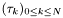 by values, then this function writes
by values, then this function writes 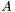 to matrix.
to matrix.
Referenced by imaging::interpolation_matrix().
| void imaging::interpolation_matrix | ( | const Bspline< float_t > & | spline, | |
| const ublas::vector< float_t > & | values, | |||
| ublas::compressed_matrix< float_t > & | matrix | |||
| ) |
#include <spline/utilities.hpp>
Computes the matrix which is the result of the spline interpolation problem. Assume a B-spline function
![\[ s(\tau) = \sum_{i = 0}^n a_i b_i(\tau) \]](form_94.png)
and consider the interpolation problem
![\[ s(\tau_k) = y_k\,,\quad 0 \leq k \leq N\,. \]](form_95.png)
Then the least squares solution of this problem is defined by the system of linear equations
![\[ \sum_{i=0}^n a_i \underbrace{\sum_{k=0}^N b_i(\tau_k)b_j(\tau_k)}_{A_{ij}} = \sum_{j=0}^N \underbrace{b_j(\tau_k)}_{B_{jk}} y_k\,,\quad 0 \leq j \leq n\,. \]](form_96.png)
If 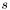 is given by spline and
is given by spline and 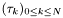 by values, then this function writes
by values, then this function writes 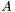 to matrix.
to matrix.
References imaging::interpolation_matrix().
| GraphicsInterface & imaging::operator<< | ( | GraphicsInterface & | out, | |
| const PeriodicBspline< ublas::fixed_vector< float_t, 2 > > & | curve | |||
| ) |
#include <spline/gio.hpp>
Draws the 2-dimensional B-Spline curve curve in the graphics output.
| GraphicsInterface & imaging::operator<< | ( | GraphicsInterface & | out, | |
| const Bspline< ublas::fixed_vector< float_t, 2 > > & | curve | |||
| ) |
#include <spline/gio.hpp>
Draws the 2-dimensional B-Spline curve curve in the graphics output.
 1.5.5
1.5.5