Linear Algebra Module


Functions
void	imaging::eigensystem (const ublas::matrix< float_t > &in, ublas::matrix< float_t > &eigenvectors, ublas::vector< float_t > &eigenvalues)
void	imaging::symmetric_square_root (const ublas::matrix< float_t > &in, ublas::matrix< float_t > &root)
void	imaging::square_root (const ublas::matrix< float_t > &in, ublas::matrix< float_t > &root)
void	imaging::inverse_square_root (const ublas::matrix< float_t > &in, ublas::matrix< float_t > &root)
void	imaging::inverse (const ublas::matrix< float_t > &in, ublas::matrix< float_t > &out)

Detailed Description

The linear algebra module provides functions for ublas::matrix and ublas::vector which are not in uBLAS. Most of the functions pass its parameters to the appropriate functions of LAPACK. Instead of being a simple wrapper of LAPACK, the functions in this module usually perform higher level task than a single LAPACK function.

Note that this module provides solver for dense systems of linear equations but not for sparse systems. Sparse solvers are collected in the linear solver module.

Function Documentation

void imaging::eigensystem	(	const ublas::matrix< float_t > &	A,
		ublas::matrix< float_t > &	eigenvectors,
		ublas::vector< float_t > &	eigenvalues
	)

#include <lapack/linear_algebra.hpp>

Computes the eigenvectors and the corresponding eigenvalues of a symmetric and positive semidefinite matrix A. The eigenvalues are sorted from the largest to the smallest. The columns of eigenvectors are ordered in the same way. If 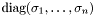$\textrm{diag}(\sigma_1, \ldots, \sigma_n)$ is the matrix with components of eigenvalues in the diagonal and 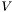$V$ denotes the matrix eigenvectors, then

$A V = V \textrm{diag}(\sigma_1, \ldots, \sigma_n)$

holds.

References imaging::max().

Referenced by imaging::inverse_square_root(), imaging::square_root(), and imaging::symmetric_square_root().

void imaging::inverse	(	const ublas::matrix< float_t > &	A,
		ublas::matrix< float_t > &	inverse
	)

#include <lapack/linear_algebra.hpp>

Computes the inverse of a non-singular matrix A.

void imaging::inverse_square_root	(	const ublas::matrix< float_t > &	A,
		ublas::matrix< float_t > &	root
	)

#include <lapack/linear_algebra.hpp>

For a symmetric and positive semidefinite matrix A, this function computes root such that if denote root as 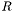$R$ the relation

$A = R^{-1}R^{-1}$

holds.

References imaging::eigensystem().

Referenced by imaging::CovarianceMatrixAdaptation::minimize().

void imaging::square_root	(	const ublas::matrix< float_t > &	A,
		ublas::matrix< float_t > &	root
	)

#include <lapack/linear_algebra.hpp>

For a symmetric and positive semidefinite matrix A, this function computes root such that if denote root as 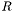$R$ the relation

$A = RR$

holds.

References imaging::eigensystem().

void imaging::symmetric_square_root	(	const ublas::matrix< float_t > &	A,
		ublas::matrix< float_t > &	root
	)

#include <lapack/linear_algebra.hpp>

For a symmetric and positive semidefinite matrix A, this function computes root such that if denote root as 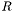$R$ the relation

$A = RR^T$

holds.

References imaging::eigensystem().

Referenced by imaging::CovarianceMatrixAdaptation::minimize().

Linear Algebra Module

Functions

Detailed Description

Function Documentation